Instituto Tecnológico de Acapulco
Departamento de metalmecánica
Unidad I
Ingeniería. Control Clásico
Equipo:
Morales
Arroyo Billy Joel
10320589
Cruz
Salas Irving
10320075
Salazar
Mesinas Luis Mario
10320092
Bahena
González Marco Antonio
10320069
Alemán
Castro Claudio
10320065
01 de octubre del 2013
1. Ser
estables y robustos frente a perturbaciones y errores en los modelos.
2. Ser
eficiente según un criterio preestablecido evitando comportamientos bruscos e
irreales.
Necesidades de la supervisión de procesos
Limitaciones
de la visualización de los sistemas de adquisición y control.
Control
vs Monitorización
Control
software. Cierre de lazo de control.
Recoger,
almacenar y visualizar información.
Clasificación de los Sistemas de
Control según su comportamiento
Definiciones
Supervisión:
acto de observar el trabajo y tareas de otro (individuo o máquina) que puede no
conocer el tema en profundidad.
1. Sistema
de control de lazo abierto: Es aquel sistema en que solo actúa el proceso
sobre la señal de entrada y da como resultado una señal de salida independiente
a la señal de entrada, pero basada en la primera. Esto significa que no hay
retroalimentación hacia el controlador para que éste pueda ajustar la acción de
control. Es decir, la señal de salida no se convierte en señal de entrada para
el controlador. Ejemplo 1: el llenado de un tanque usando una manguera de
jardín. Mientras que la llave siga abierta, el agua fluirá. La altura del agua
en el tanque no puede hacer que la llave se cierre y por tanto no nos sirve
para un proceso que necesite de un control de contenido o concentración.
Ejemplo 2: Al hacer una tostada, lo que hacemos es controlar el tiempo de
tostado de ella misma entrando una variable (en este caso el grado de tostado
que queremos). En definitiva, el que nosotros introducimos como parámetro es el
tiempo.
Estos
sistemas se caracterizan por:
- Ser
sencillos y de fácil concepto.
- Nada
asegura su estabilidad ante una perturbación.
- La
salida no se compara con la entrada.
- Ser
afectado por las perturbaciones. Éstas pueden ser tangibles o intangibles.
- La
precisión depende de la previa calibración del sistema.
2. Sistema de control de lazo cerrado: Son los sistemas en los que la
acción de control está en función de la señal de salida. Los sistemas de
circuito cerrado usan la retroalimentación desde un resultado final para
ajustar la acción de control en consecuencia. El control en lazo cerrado es
imprescindible cuando se da alguna de las siguientes circunstancias:
- Cuando
un proceso no es posible de regular por el hombre.
- Una
producción a gran escala que exige grandes instalaciones y el hombre no es
capaz de manejar.
- Vigilar
un proceso es especialmente difícil en algunos casos y requiere una atención
que el hombre puede perder fácilmente por cansancio o despiste, con los
consiguientes riesgos que ello pueda ocasionar al trabajador y al proceso.
Sus
características son:
- Ser
complejos, pero amplios en cantidad de parámetros.
- La
salida se compara con la entrada y le afecta para el control del sistema.
- Su
propiedad de retroalimentación.
- Ser
más estable a perturbaciones y variaciones internas.
Un
ejemplo de un sistema de control de lazo cerrado sería el termotanque de agua
que utilizamos para bañarnos. Otro ejemplo sería un regulador de nivel de gran
sensibilidad de un depósito. El movimiento de la boya produce más o menos
obstrucción en un chorro de aire o gas a baja presión. Esto se traduce en
cambios de presión que afectan a la membrana de la válvula de paso, haciendo
que se abra más cuanto más cerca se encuentre del nivel máximo.
Diagrama de bloques
diagrama de bloques es la representación gráfica del funcionamiento
interno de un sistema, que se hace mediante bloques y sus relaciones, y que,
además, definen la organización de todo el proceso interno, sus entradas y sus
salidas.
Un
diagrama de bloques de procesos de producción es un diagrama utilizado para
indicar la manera en la que se elabora cierto producto, especificando la
materia prima, la cantidad de procesos y la forma en la que se presenta el
producto terminado.
Un
diagrama de bloques de modelo matemático es el utilizado para representar el
control de sistemas físicos (o reales) mediante un modelo
matemático, en el cual, intervienen gran cantidad de
variables que se relacionan en todo el proceso de producción. El modelo
matemático que representa un sistema físico de alguna complejidad conlleva a la
abstracción entre la relación de cada una de sus partes, y que conducen a la
pérdida del concepto global. En ingeniería de control, se han desarrollado una
representación gráfica de las partes de un sistema y sus interacciones. Luego
de la representación gráfica del modelo matemático, se puede encontrar la
relación entre la entrada y la salida del proceso del sistema.
Sistema lineal
En esta actividad podrás elegir el sistema lineal (dos
ecuaciones del tipo a x + b y = c
o equivalentes) a resolver y el método de resolución, ver sus pasos y comprobar
tus resultados. Recuerda que antes de aplicar algún método en tu cuaderno tal
vez necesites una preparación previa de cada ecuación, como quitar paréntesis o
agrupar y ordenar los términos.
Recuerda también que gracias a las ecuaciones en ningún
momento estás realmente obligado a realizar operaciones con fracciones. En caso
de aparecer, puedes convertirlas en enteros multiplicando toda la ecuación por
el producto de los denominadores que hubiera, o, si te resulta sencillo
calcularlo mentalmente, por su mínimo común múltiplo.
Instrucciones de uso: Para introducir un nuevo sistema como introduce la primera ecuación en la barra de Entrada con el nombre de e1. Por ejemplo:
e1: 2x - 3y = 3
(u otra equivalente, como e1:
y = 2x/3 -1) y después introduce la segunda ecuación con el nombre de e2.
Por ejemplo:
e2: 3x - y = 1
Notas:
·
Cuando las rectas sean
coincidentes o paralelas, o alguna sea horizontal o vertical, la resolución es
la misma en todos los casos.
·
En caso de introducir
coeficientes racionales no enteros, la aplicación mostrará automáticamente una
ecuación equivalente con coeficientes enteros.
·
Puedes recuperar las ecuaciones
introducidas en la barra de Entrada haciendo clic en ella y pulsando las teclas
↑ y ↓.
Sistemas lineales
variables con el tiempo
En esta
tesis doctoral se aborda el control de sistemas no lineales mediante el empleo
de controladores predictivos generalizados (GPCs) en espacio de estados. En
primer lugar se realiza una revisión de la metodología de diseño del GPC en la
versión entrada/salida (E/S). Partiendo de esta revisión se propone un modelo
CARIMA en espacio de estados para el GPC que permite diseñar al mismo
utilizando una menor cantidad de memoria y un menor tiempo de cómputo, así como
de reducir la complejidad asociada la formulación E/S. Para la estimación de
los estados del modelo CARIMA se propone el uso de un observador de rango
completo que se diseña por asignación de polos, estableciéndose un importante
resultado: los polos de este observador coinciden con las raíces de los
polinomios de filtrado utilizados en la formulación E/S. Posteriormente se
analizan las propiedades de observabilidad y controlabilidad del modelo CARIMA
propuesto en espacio de estados, llegándose a la conclusión de que se trata de
una realización mínima bajo condiciones no demasiado restrictivas, lo cual
supone que la predicción se basa en un modelo con el mínimo orden posible.
Tras
esto, se presenta una metodología de análisis y diseño estable para el GPC
mediante el uso del índice de coste como función de Lyapunov, y para el caso
con restricciones de la teoría de conjuntos invariantes aplicada al GPC.
Seguidamente,
se presenta una metodología de diseño robusto para el GPC mediante el empleo de
las desigualdades lineales matriciales (LMIs) y de algoritmos genéticos. En
concreto, se analiza el caso de sistemas con incertidumbre invariante y
variante con el tiempo de tipo lineal fraccional, una de las más complejas y
generales utilizadas en la literatura analizada.
Finalmente
se presenta el controlador GPC-LPV una extensión del GPC en espacio de estados.
Se trata de un controlador variante con el tiempo que presenta dependencia
lineal fraccional con respecto de las señales de salida medibles. Su diseño es
No linealidad
En matemáticas, los sistemas
no lineales representan sistemas cuyo comportamiento no es expresable como
la suma de los comportamientos de sus descriptores. Más formalmente, un sistema
físico, matemático o de otro tipo es no lineal cuando las ecuaciones
de movimiento, evolución o comportamiento que regulan su
comportamiento son no lineales. En particular, el comportamiento de sistemas no
lineales no está sujeto al principio de superposición, como lo
es un sistema
lineal.
La
linealidad de un sistema permite a los investigadores hacer ciertas
suposiciones matemáticas y aproximaciones, permitiendo un cálculo más sencillo
de los resultados. Ya que los sistemas no lineales no son iguales a la suma de
sus partes, usualmente son difíciles (o imposibles) de modelar, y sus
comportamientos con respecto a una variable dada (por ejemplo, el tiempo) es
extremadamente difícil de predecir.
Algunos
sistemas no lineales tienen soluciones exactas o integrables, mientras que
otros tienen comportamiento caótico, por lo tanto no se pueden reducir a una
forma simple ni se pueden resolver. Un ejemplo de comportamiento caótico son
las olas
gigantes. Aunque algunos sistemas no lineales y ecuaciones de interés general
han sido extensamente estudiados, la vasta mayoría son pobremente comprendidos.
Linealización
En general el proceso de linealización quiere
decir que la representación matemática de un problema tenga una aproximación
lineal, o que por medio de un cambio de variables el problema se haga lineal,
en el sentido que las ecuaciones correspondientes contengan sólo la primera
potencia de las variables involucradas en el sistema considerado.
Por ejemplo, la ecuación de un péndulo plano
es
segunda derivada del ángulo con respecto al
tiempo = - constante por el seno del ángulo
θ''=-c senθ, la cual es una ecuación no
lineal que se puede llevar a un problema lineal cuando θ<<1, ya que en
este caso senθ ≈ θ; por lo tanto, en el caso de ángulo pequeños tenemos que la
ecuación es lineal
UNIDAD 2 MODELADOS DE
SISTEMAS MECANICOS
2.1 FUNCIÓN DE TRANSFERENCIA
Una función de transferencia es un modelo matemático que a través de un cociente relaciona la
respuesta de un sistema (modelada) a una señal de entrada o excitación
(también modelada). En la teoría de control, a menudo se usan las funciones de
transferencia para caracterizar las relaciones de entrada y salida de
componentes o de sistemas que se describen mediante ecuaciones diferenciales
lineales e invariantes en el tiempo.
Definicion
La
podemos definir formalmente como:
La
función de trasferencia de un sistema lineal e invariante en el tiempo (LTI),
se define como el cociente entre la transformada de Laplace de la salida y la
transformada de Laplace de la entrada, bajo la suposición de que las
condiciones iniciales son nulas.
El
pico formado por los modelos de la señal de salida respecto de la señal de
entrada, permite encontrar los ceros y los polos, respectivamente. Y que
representan las raíces en las que cada uno de los modelos del cociente se
iguala a cero. Es decir, representa la región frontera a la que no debe llegar
ya sea la respuesta del sistema o la excitación al mismo; ya que de lo
contrario llegará ya sea a la región nula o se irá al infinito,
respectivamente.
Considerando
la temporalidad; es decir, que la excitación al sistema tarda un tiempo en
generar sus efectos en el sistema en cuestión y que éste tarda otro tiempo en
dar respuesta. Esta condición es vista a través de un proceso de convolución, formado por la excitación de entrada
convolucionada con el sistema considerado, dando como resultado, la respuesta
dentro de un intervalo de tiempo. Ahora, en ese sentido (el de la convolución), se tiene que observar que la función de
transferencia está formada por la deconvolución entre la señal de entrada con el sistema.
Dando como resultado la descripción externa de la operación del sistema
considerado. De forma que el proceso de contar con la función de transferencia
del sistema a través de la deconvolución, se logra de forma matricial o
vectorial, considerando la pseudoinversa de
la matriz o vector de entrada multiplicado por el vector de salida, para
describir el comportamiento del sistema dentro de un intervalo dado. Pareciera
un proceso complicado, aunque solo baste ver que la convolución discreta es
representada por un producto de un vector o matriz fija respecto de una matriz
o vector móvil, o que en forma tradicional se observa como una sumatoria.
Descripcion matemática
Uno
de los primeros matemáticos en describir estos modelos fue La place, a través de su transformación matemática.
Por
definición una función de transferencia se puede determinar según la expresión:
donde H
(s) es la función de transferencia (también notada
como G (s) ); Y (s) es la transformada
de Laplace de la respuesta
y X (s) es la transformada
de Laplace de la señal
de entrada.
La
función de transferencia también puede considerarse como la respuesta de un
sistema inicialmente inerte a un impulso como
señal de entrada:
La
salida o respuesta en frecuencia del sistema se halla entonces de
Y(s) = H (s) X(s)
Cualquier
sistema físico (mecánico, eléctrico, etc.) se puede traducir a una serie de
valores matemáticos a través de los cuales se conoce el comportamiento de estos
sistemas frente a valores concretos.
Por
ejemplo, en análisis de circuitos eléctricos, la función de transferencia se
representa como:
SISTEMAS MECANICOS
Se caracterizan
por presentar elementos o piezas sólidos, con el objeto de realizar movimientos
por acción o efecto de una fuerza.
En ocasiones, pueden asociarse con sistemas eléctricos y producir movimiento a partir de un motor accionado por la energía eléctrica.
En general la mayor cantidad de sistemas mecánicos usados actualmente son propulsados por motores de combustión interna.
En los sistemas mecánicos. se utilizan distintos elementos relacionados para transmitir un movimiento.
Como el movimiento tiene una intensidad y una dirección, en ocasiones es necesario cambiar esa dirección y/o aumentar la intensidad, y para ello se utilizan mecanismos.
En general el sentido de movimiento puede ser circular (movimiento de rotación) o lineal (movimiento de translación) los motores tienen un eje que genera un movimiento circular
En ocasiones, pueden asociarse con sistemas eléctricos y producir movimiento a partir de un motor accionado por la energía eléctrica.
En general la mayor cantidad de sistemas mecánicos usados actualmente son propulsados por motores de combustión interna.
En los sistemas mecánicos. se utilizan distintos elementos relacionados para transmitir un movimiento.
Como el movimiento tiene una intensidad y una dirección, en ocasiones es necesario cambiar esa dirección y/o aumentar la intensidad, y para ello se utilizan mecanismos.
En general el sentido de movimiento puede ser circular (movimiento de rotación) o lineal (movimiento de translación) los motores tienen un eje que genera un movimiento circular
Ejemplo de de
elementos que lo integran:
Polea simple : la
polea simple se encarga solamente de invertir el sentido de la fuerza aplicada.
Por lo tanto no existe ventaja mecánica, sólo puede haber pérdidas debidas al
rozamiento.
Palanca: Generalmente
está formada por una barra rígida que puede oscilar en torno a una pieza fija,
que sirve de punto de apoyo.
Palanca de primer
grado, palanca de segundo grado
palanca
de tercer grado: palancas de tercer Grado, el punto de apoyo se sitúa
en un extremo de la barra, la fuerza resistente en el otro extremo, y la fuerza
se aplica en una posición intermedia
el polipasto: El
polipasto es una máquina simple que se usa para levantar cargas muy pesadas a
una cierta altura. Está formado por un bloque de poleas fijo al techo, y otro
bloque de poleas móvil, acoplado al primer bloque mediante una cuerda. Se usa
de forma similar a la polea simple, pero en el caso del polipasto la fuerza que
hay que aplicar es menor, de manera que se consigue una ventaja mecánica.
el torno o cabestrante: es una maquina simple formada por un tambor
con una cuerda y una manivela, que se usa para levantar cargas hasta la altura
del tambor. Cuando el brazo de la manivela es más largo que el diámetro del
tambor, existe ventaja mecánica.
2.1.1.1 DE
TRANSLACION Y ROTACION
Son dispositivos que se pueden considerar convertidores de movimiento,
en tanto transforman el movimiento de una y otra forma.
Entre los elementos mecánicos están los mecanismos de barras
articuladas, levas, engranes, cremalleras, cadenas, correas de transmision...
Los sistemas antiguos de mecánica con el paso del tiempo están siendo
desplazados por los sistemas electrónicos. Pero bien algunos sistemas mecánicos
son más factibles de utilizar como:
Amplificación de fuersas
Cambio de velocidad
Transferencia de rotación de un eje a otro
Determinates tipos de movimiento
Tipos de movimientos
Para poder describir el movimiento rotacional y de traslación en la
mecánica se representan mediante tres ejes (X,Y,Z).
para poder comprender los movimiento dentro del lenguaje de la ing.
mecánica de una actividad tan simple como levantar un lápiz que esta sobre la
mesa, resulta un tanto complicado por que se debe de tener en cuenta todos los
movimientos de rotación y desplazamiento de se realizan.
Grados de libertad y de restricción
Uno de los aspectos importantes de la mecánica es el diseño de los
elementos es la orientación y disposición de elementos y partes. Los grados de
libertad es la cantidad necesaria de componentes de movimiento para producir el
movimiento correspondiente.
Un problema del diseño es reducir los grados de libertad para eso se
deben de tener en cuenta las restricciones se pueden tener hasta 6 grados de
libertad si no se tienen ninguna restricción
La carga es un aspecto importante dentro del diseño mecánico por que de
aquí parte de que dimensiones debe ser la pieza y una serie de elementos los
cuales se deben de tener en cuenta dentro del diseño.
Cadenas cinemática
Las articulaciones son mecanismos a los cuales no séle toman en cuenta
la fuerza. Esta no tiene por fuerza que ser un cuerpo rígido, basta que sea un
cuerpo resistente capaz de transmitir la fuerza requerida sufriendo una
deformación despreciable.
Los pistones, la biela, correas y poleas son ejemplos de articulaciones.
La cadena cinemática es el conjunto de piezas de eslabonamiento y de
articulaciones una articulación debe de ser fija.
La cadena de cuatro barras
Esta cadena consiste en cuatro acoplamientos conectados entre si de
manera que producen cuatro piezas de enlace, cada una de las cuales tiene la
posibilidad de girar.
TRENES DE ENGRANE
Son mecanismos utilizados para transferir y transformar el movimiento
rotacional. Se emplean cuando es necesario obtener un cambio en la velocidad, o
el par de rotación de un dispositivo que esta girando.
La fuerza de fricción en un elemento muy importante dentro de los
engranes. Para poder evitar que existan derrapes o desplazamientos se le agrega
a los dos cuerpos cilíndricos una serie de dientes de engrane.
El piñón y la cremallera es un conjunto de dos partes una un engrane
cilíndrico y un engrane lineal el cual hace un movimiento de rotacional a
lineal y lineal a rotacional.
Cuando se tienen dos engranes conectados sirven para transferir la
velocidad de rotación a una velocidad deseada todo esto depende del tamaño de
los engranes y de la cantidad de dientes con la que cuente cada engrane.
RUEDA DENTADA Y TRINQUETE
Se utilizan para trabar un mecanismo cuando sostiene una carga. El
mecanismo cuenta con una rueda dentada con dientes de forma de sierra que se
enganchan con un sierre denominado trinquete. Esta esta sujeto a un pivote y se
mueve hacia arriba y hacia abajo para trabar la rueda. La forma de los dientes
permite la rotación hacia un solo sentido. El trinque impide la rotación de la
rueda dentada en el sentido de las manecias del reloj y solo puede hacerlo
levantando el trinquete, el cual casi siempre se acciona con el resorte para
garantizar que de manera automática quede trabado en los dientes de la rueda
dentada.
Transmisión por correa dentada
Es la transmisión de un movimiento giratorio de un cuerpo cilíndrico a
otro mediante una correa con dientes. Las ventajas de este sistema de
transmisión de movimiento es que los dos cuerpos cilíndricos pueden estar
retirados.
Existen varios tipos de correas como:
Plana, redonda, en V y correa dentada reguladora de tiempo.
Cadenas.
Se utilizan para evitar un deslizamiento, las cadenas se enganchan con
los dientes de los engranes y con este enganchamiento se logra transmitir el
movimiento. La desventaja es que no es tan silenciosa.
Chumaceras
Las chumaceras o cojinetes tienen la función de girar el movimiento de
una parte respecto de otra con mínima fricción y máxima exactitud.
SISTEMAS ELECTRICOS
Es una serie de
elementos o componentes eléctricos o electrónicos, tales como resistencias,
inductancias, condensadores, fuentes,
y/o dispositivos electrónicos semiconductores,
conectados eléctricamente entre sí con el propósito de generar, transportar o
modificar señales electrónicas
o eléctricas.
Un circuito
eléctrico tiene que tener estas partes, o ser parte de ellas.
3. Por el tipo de
componentes: Eléctricos: Resistivos, inductivos, capacitivos y mixtos.
Electrónicos: digitales, analógicos y mixtos.
4. Por su
configuración: En Serie y Paralelo.
·
1. Todo
circuito eléctrico está formado por una fuente de energía (tomacorriente),
conductores (cables), y un receptor que transforma la electricidad en luz (lámparas),en movimiento (motores),
en calor (estufas).
·
2. Para que
se produzca la transformación, es necesario que circule corriente por el
circuito.
3. Este debe estar
compuesto por elementos conductores, conectados a una fuente de tensión o
voltaje y cerrado.
4. Los
dispositivos que permiten abrir o cerrar circuitos se llaman interruptores o
llaves.
·
Conductor
eléctrico: Cualquier material que ofrezca poca resistencia
al flujo de electricidad se denomina conductor eléctrico. La diferencia entre
un conductor y un aislante, que es un mal conductor de electricidad o de calor,
es de grado más que de tipo, ya que todas las sustancias conducen electricidad
en mayor o en menor medida. Un buen conductor de electricidad, como la plata o
el cobre,
puede tener una conductividad mil millones de veces superior a la de un buen aislante,
como el vidrio o
la mica. En los conductores sólidos la corriente eléctrica es
transportada por el movimiento de los electrones; y en disoluciones y gases,
lo hace por los iones.
Los materiales en
los que los electrones están fuertemente ligados a los átomos se conocen como
aislantes, no conductores o dieléctricos. Algunos ejemplos son el vidrio, la
goma o la madera seca.
REPRESENTACION EN DIAGRAMAS DE BLOQUE A LAZO
CERRADO
Un sistema de
control puede tener varios componentes. Para mostrar lasfunciones que lleva a
cabo cada componente en la ingeniería de control, por logeneral se usa una
representación denominada diagrama de bloques. Estosdiagramas de bloques
también representan el flujo de señales entre los bloques,de manera que indican
el camino de la información, sea del tipo que sea. Adiferencia de una
representación matemática puramente abstracta, un diagramade bloques tiene la
ventaja de indicar en forma más realista el flujo de las señalesdel sistema
real.En un diagrama de bloques se enlazan
una con otras todas las variables delsistema, mediante bloques funcionales. El
bloque funcional o simplemente bloquees un símbolo para representar la
operación matemática que sobre la señal deentrada hace el bloque para producir
la salida. Las funciones de transferencia delos componentes por lo general se
introducen en los bloques correspondientes,que se conectan mediante flechas
para indicar la dirección de flujo de las señales.En la figura observe que la
señal sólo puede pasar en dirección de las flechas. Por lo tanto, un
diagrama de bloques de un sistema de control muestra explícitamenteuna propiedad unilateral.
SISTEMAS
ANALOGOS
Los circuitos electrónicos
se pueden dividir en dos amplias categorías: digitales y analógicos. La electrónica digital
utiliza magnitudes con valores discretos,
mientras que la electrónica analógica emplea magnitudes con valores continuos.
Un sistema
digital es cualquier dispositivo destinado a la generación,
transmisión, procesamiento o almacenamiento de señales digitales.
También un sistema digital es una combinación de dispositivos
diseñado para manipular cantidades físicas o información que
estén representadas en forma digital; es decir, que sólo puedan tomar valores
discretos.
La mayoría de las
veces estos dispositivos son electrónicos, pero también pueden ser mecánicos,
magnéticos o neumáticos.
Para el análisis y
la síntesis de sistemas digitales
binarios se utiliza como herramienta el álgebra de
Boole.
Los sistemas
digitales pueden ser de dos tipos:
·
·
Sistemas digitales
combinacionales: Son aquellos en los que la
salida del sistema sólo depende de la entrada presente. Por lo tanto, no
necesita módulos de memoria,
ya que la salida no depende de entradas previas.
·
·
Sistemas digitales
secuenciales: La salida depende de la
entrada actual y de las entradas anteriores. Esta clase de
sistemas necesitan elementos de memoria que recojan la información de la 'historia pasada'
del sistema.
Para la
implementación de los circuitos digitales, se utilizan puertas lógicas (AND, OR
y NOT) y transistores.
Estas puertas siguen el comportamiento de
algunas funciones booleanas.
Se dice que
un sistema es analógico cuando las magnitudes
de la señal se representan mediante variables continuas,
esto es análogas a las magnitudes que dan lugar a la
generación de esta señal. Un sistema analógico contiene
dispositivos que manipulan cantidades físicas representadas en forma analógica.
En un sistema de este tipo, las cantidades varían sobre un intervalo continuo
de valores.
Así, una magnitud
analógica es aquella que toma valores continuos. Una magnitud digital es
aquella que toma un conjunto de valores discretos.
La mayoría de las
cosas que se pueden medir cuantitativamente aparecen en la naturaleza en
forma analógica. Un ejemplo de ello es la temperatura:
a lo largo de un día la temperatura no varía entre, por ejemplo, 20 ºC o 25 ºC
de forma instantánea, sino que alcanza todos los infinitos valores que entre
ese intervalo. Otros ejemplos de magnitudes analógicas son el tiempo,
la presión,
la distancia, el sonido.
Una señal
analógica es un voltaje o corriente que varía suave y continuamente. Una onda
senoidal es una señal analógica de una sola frecuencia. Los voltajes de la voz
y del video son
señales analógicas que varían de acuerdo con el sonido o variaciones de
la luz que
corresponden a la información que se está transmitiendo.
ANALOGIA FUERZA TENSION
Para comprender las analogías vamos a ver un caso
sencillo de un circuito mecánico con un grado de libertad. No importa en ningún
caso la complejidad de los sistemas, solo importa que las ecuaciones que rigen
su comportamiento sean iguales.
Sea el siguiente sistema
mecánico de traslación:
En este sistema M es la masa, R el coeficiente
de rozamiento o amortiguamiento, K la constante de elasticidad del muelle, x el
desplazamiento lineal y F la fuerza aplicada. La ecuación diferencial que
define su comportamiento es:
(Expresión A)
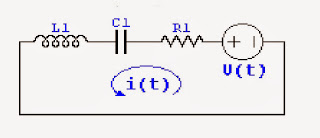
Sea el siguiente sistema eléctrico pasivo:
En este sistema L es la inductancia de la
bobina, R la resistencia, C la capacidad del condensador, i la corriente que
circula y V la tensión aplicada. La ecuación integro-diferencial que rige su
comportamiento es:
que puede ponerse en términos de la carga eléctrica
q como:
A la vista de las expresiones A
y B es evidente que las ecuaciones diferenciales para ambos sistemas son idénticas,
por lo que estos sistemas se denominan sistemas análogos, y las magnitudes que
los representan se llaman magnitudes análogas.
Esta correspondencia es
conocida como analogía de impedancia, o Fuerza-Tensión, y se representa en
la siguiente tabla:
ANALOGIA FUERZA CORRIENTE
Establecer
la relación existente entre las ecuaciones de fuerza de un sistema mecánicoy un sistema eléctrico. Las ecuaciones que
describen el sistema para el circuitoeléctrico son:Figura 2.2que expresa
da en términos del flujo magnético nos da:(2.4)Dado que el sistema mecánico ha sido considerado el mismo que para la
analogíafuerza voltaje podemos comparar (1.36) y (1.38) para obtener obtenemos lasrelaciones
dadas en la siguiente tabla que son denominadas analogías.
MOTORES DE CC CONTROLADOS POR EL
INDUCIDO
El
motor de corriente continua es una máquina que convierte la energía eléctrica
en mecánica, provocando un movimiento rotatorio. En algunas modificaciones,
ejercen tracción sobre un riel. Estos motores se conocen como motores lineales
Su principal inconveniente, el mantenimiento, muy caro y laborioso.
Una
máquina de corriente continua (generador o motor) se compone principalmente de
dos partes, un estátor que da soporte mecánico al aparato y tiene un hueco en
el centro generalmente de forma cilíndrica. En el estátor además se encuentran
los polos, que pueden ser de imanes permanentes o devanados con hilo de cobre
sobre núcleo de hierro. El rotor es generalmente de forma cilíndrica, también
devanado y con núcleo, al que llega la corriente mediante dos escobillas.
También
se construyen motores de CC con el rotor de imanes permanentes para
aplicaciones especiales.
Según
la ley de Fuerza de Lorentz simplificada,
cuando un conductor por el que pasa una corriente eléctrica se sumerge en un campo
magnético, el conductor sufre una fuerza perpendicular
al plano formado por el campo magnético y la corriente, siguiendo la regla de la mano derecha.
·
l: Longitud del conductor en metros
El
rotor tiene varios repartidos por la periferia. A medida que gira, la corriente
se activa en el conductor apropiado.
Normalmente
se aplica una corriente con sentido contrario en el extremo opuesto del rotor,
para compensar la fuerza neta y aumentar el momento.
Fuerza contraelectromotriz inducida en un
motor
Es la
tensión que se crea en los conductores de un motor como consecuencia del corte
de las líneas de fuerza, es el efecto generador de pines.
La
polaridad de la tensión en los generadores es inversa a la aplicada en bornes
del motor.
Las
fuertes puntas de corriente de un motor en el arranque son debidas a que con la
máquina parada no hay fuerza contraelectromotriz y el bobinado se comporta como
una resistencia pura del circuito.
La
fuerza contraeloectromotriz en el motor depende directamente de la velocidad de
giro del motor y del flujo magnetico del sistema inductor.
Número de escobillas
Las escobillas deben
poner en cortocircuito todas las bobinas situadas en la zona neutra. Si la
máquina tiene dos polos, tenemos también dos zonas neutras. En consecuencia, el
número total de escobillas ha de ser igual al número de polos de la máquina. En
cuanto a su posición, será coincidente con las líneas neutras de los polos.
sentido de giro
El
sentido de giro de un motor de corriente continua depende del sentido relativo
de las corrientes circulantes por los devanados inductor e inducido.
La
inversión del sentido de giro del motor de corriente continua se consigue
invirtiendo el sentido del campo magnético o de la corriente del inducido.
Si se
permuta la polaridad en ambos bobinados, el eje del motor gira en el mismo
sentido.
Los
cambios de polaridad de los bobinados, tanto en el inductor como en el inducido
se realizarán en la caja de bornes de la máquina, y además el ciclo combinado
producido por el rotor produce la fuerza magnetomotriz.
El
sentido de giro lo podemos determinar con la regla de la mano derecha, la cual
nos va a mostrar el sentido de la fuerza. La regla de la mano derecha es de la
siguiente manera: el pulgar nos muestra hacia donde va la corriente, el dedo
índice apunta en la dirección en la cual se dirige el flujo del campo
magnético, y el dedo medio hacia donde va dirigida la fuerza resultante y por
lo tanto el sentido de giro.
MOTORES DE CC CONTROLADOS POR EL CAMPO
Los motores eléctricos
de corriente continua son el tema de base que se amplia en el siguiente trabajo,
definiéndose en el mismo los temas de más relevancia para el caso de los
motores eléctricos de corriente continua, como lo son: su definición, los tipos
que existen, su utilidad,
distintas partes que los componen, clasificación por excitación, la velocidad,
la caja de bornes y otros mas.
Esta máquina de
corriente continua es una de las más versátiles en la industria.
Su fácil control de
posición, par y velocidad la han convertido en una de las mejores opciones en
aplicaciones de control y automatización de procesos.
Pero con la llegada de la electrónica su
uso ha disminuido en gran medida, pues los motores de corriente alterna, del
tipo asíncrono, pueden ser controlados de igual forma a precios más
accesibles para el consumidor medio
de la industria. A pesar de esto los motores de corriente continua se siguen
utilizando en muchas aplicaciones de potencia (trenes
y tranvías) o de precisión (máquinas,
micro motores, etc.)
Un motor eléctrico
de Corriente Continua es esencialmente una máquina que convierte energía
eléctrica en movimiento o
trabajo mecánico, a través de medios electromagnéticos.
FUNDAMENTOS DE
OPERACIÓN DE LOS MOTORES ELÉCTRICOS
En magnetismo se
conoce la existencia de dos polos: polo
norte (N) y polo sur (S), que
son las regiones donde se concentran las líneas de fuerza de
un imán. Un motor para funcionar se vale de las fuerzas de atracción y
repulsión que existen entre los polos. De acuerdo con esto, todo motor tiene
que estar formado con polos alternados entre el estator y el rotor, ya que los
polos magnéticos iguales se repelen, y polos magnéticos diferentes se atraen,
produciendo así el movimiento de rotación.
Un motor eléctrico
opera primordialmente en base a dos principios:
El de inducción,
descubierto por Michael Faraday en 1831; que señala, que si un conductor se
mueve a través de un campo magnético o está situado en las proximidades de otro
conductor por el que circula una corriente de intensidad variable, se induce
una corriente eléctrica en el primer conductor. Y el principio que André Ampére
observo en 1820, en el que establece: que si una corriente pasa a través de un
conductor situado en el interior de un campo
magnético, éste ejerce una fuerza mecánica o
f.e.m. (fuerza electromotriz), sobre el conductor.
El movimiento
giratorio de los motores de C.C. se basa en el empuje derivado de la repulsión
y atracción entre polos magnéticos. Creando campos constantes convenientemente
orientados en estator y rotor, se origina un par de fuerzas que obliga a que la
armadura (también le llamamos así al rotor) gire buscando "como loca"
la posición de equilibrio.
Gracias a un juego de
conexiones entre unos conductores estáticos, llamados escobillas, y las bobinas
que lleva el rotor, los campos magnéticos que produce la armadura cambian a
medida que ésta gira, para que el par de fuerzas que la mueve se mantenga
siempre vivo.
Se utilizan en
casos en los que es importante el poder regular
continuamente la velocidad del motor, además, se utilizan en aquellos casos en
los que es imprescindible utilizar corriente directa, como es el caso de
motores accionados por pilas o
baterías. Este tipo de motores debe de tener en el rotor y el estator el mismo
numero de polos y el mismo numero de carbones.
LOS MOTORES DE
CORRIENTE DIRECTA PUEDEN SER DE TRES TIPOS:
·
SERIE
·
PARALELO
·
COMPOUND
MOTOR SERIE: es
un tipo de motor eléctrico de corriente continua en el cual el devanado de
campo (campo magnético principal) se conecta en serie con la armadura. Este
devanado está hecho con un alambre grueso porque tendrá que soportar la
corriente total de la armadura.
Debido a esto se
produce un flujo magnético proporcional a la corriente de armadura (carga del
motor). Cuando el motor tiene mucha carga, el campo de serie produce un campo
magnético mucho mayor, lo cual permite un esfuerzo de torsión mucho
mayor. Sin embargo, la velocidad de giro varía dependiendo del tipo de carga
que se tenga (sin carga o con carga completa). Estos motores desarrollan un par
de arranque muy elevado y pueden acelerar cargas pesadas rápidamente.
ESPACIO DE ESTADOS RELACION ENTRE FUNCION DE
TRANSFERENCIAY ESPACIO DE ESTADOS
En ingeniería de control, una representación de espacios de
estados es un modelo
matemático de un sistema físico descrito mediante un conjunto de entradas,
salidas y variables de estado relacionadas por ecuaciones diferenciales de primer orden que se combinan en una
ecuación diferencial matricial de primer orden. Para prescindir del
número de entradas, salidas y estados, las variables son expresadas como vectores y las ecuaciones algebraicas se escriben
en forma matricial (esto último sólo puede hacerse cuando el sistema dinámico es lineal e invariante en el tiempo). La
representación de espacios de estado (también conocida como aproximación en el dominio del
tiempo) provee un modo compacto y conveniente de modelar y analizar
sistemas con múltiples entradas y salidas. Con entradas y 
salidas, tendríamos que escribir 
veces la transformada de Laplace para procesar toda la información del
sistema. A diferencia de la aproximación en el dominio de la frecuencia, el uso
de la representación de espacios de estado no está limitada a sistemas con
componentes lineales ni con condiciones iniciales iguales a cero. El espacio de estado se refiere al espacio de 
dimensiones cuyos ejes coordenados están
formados por variables de estados. El estado del sistema puede ser representado
como un vector dentro de ese espacio.
entradas y salidas, tendríamos que escribir veces la transformada de Laplace para procesar toda la información del
sistema. A diferencia de la aproximación en el dominio de la frecuencia, el uso
de la representación de espacios de estado no está limitada a sistemas con
componentes lineales ni con condiciones iniciales iguales a cero. El espacio de estado se refiere al espacio de dimensiones cuyos ejes coordenados están
formados por variables de estados. El estado del sistema puede ser representado
como un vector dentro de ese espacio.
Las variables de estado son el subconjunto más pequeño de
variables de un sistema que pueden representar su estado dinámico completo en
un determinado instante. Estas variables de estado deben ser linealmente
independientes; una variable de estado no puede ser una combinación lineal de
otras variables de estado. El número mínimo de variables de estado necesarias
para representar un sistema dado, n,
es normalmente igual al orden de la ecuación diferencial que define al sistema.
Si el sistema es representado en forma de función de
transferencia, el número mínimo de variables de estado es igual al
orden del denominador de la función transferencia después de haber sido
reducido a una fracción propia. Cabe destacar que al convertir una
representación de espacio de estado a la forma de función de transferencia
puede perderse información interna sobre el sistema, pudiendo por ejemplo
describir un sistema como estable aun cuando la representación de espacio de estado
indica que es inestable en ciertos puntos. En circuitos eléctricos, el número
de variables de estado es a menudo, pero no siempre, igual al número de
elementos almacenadores de energía, comobobinas y condensadores.
EJEMPLOS EN SISTEMAS
ELÉCTRICOS Y MECÁNICOS EN EL MODELO MATEMÁTICO
UNIDAD 3 RESPUESTA DINÁMICA
MAPA CONCEPTUAL
UNIDAD 4 ACCIONES BÁSICAS DE CONTROL
MAPA CONCEPTUAL
UNIDAD 5 ESTABILIDAD
MAPA CONCEPTUAL
No hay comentarios:
Publicar un comentario